(Last updated at Mar 23 2024)

Comparing performance of sequential and random insertions to a B-tree

I read this interesting article about choosing primary keys (PK) in Postgres. The article mentions that using UUID as PK causes performance drop w.r.t. to a serial (autoincrementing integer) PK:

[…] when you use Postgres native UUID v4 type instead of bigserial table size grows by 25% and insert rate drops to 25% of bigserial.

Back when I worked in Amazon I recall a tech talk that mentioned that using a UUID keys instead of serial keys causes performance drops for databases that use B-tree, because insertions of UUID to a B-tree are less cache-friendly than inserting serial integers.

I decided to explore the topic further, so I implemented a B-tree and run some benchmarks. I could measure the performance directly (with Go benchmark), I wanted also to somehow measure “cache friendliness”. To measure cache friendliness, I checked times when a node of the B-tree was last accessed, where the “time” is just a tick of an integer counter. The intuition behind the measurement is that when a node is accessed more frequently (less “ticks” between the accesses), there is a larger chance that the node is still in cache. The more “ticks” between the subsequent accesses of the mode, the more chance the node was evicted from the cache. The less “ticks” between the accesses of the nodes overall, the structure (or the insert pattern) is more cache-friendly.

Performance

The original article mentions inserting UUIDs. My simplistic B-tree implementation does not support UUIDs, so I compared insertion of a serial type (an incrementing sequence of integers) and a shuffled sequence of integers. The assumption here is that the shuffled sequence would emulate how semi-random UUID (or a hash of it) is inserted to the tree.

The table summaries the time it takes to insert 100k keys to B-trees of different B-tree order. The “degradation” is the time it takes to insert the shuffled sequence t_shuf compared to time it takes to insert the straight sequence t_seq:

degradation = (time for shuffled sequence) / (time for straight sequence) - 1

B-tree order	degradation
2	156.6%
3	17.5%
6	17.0%
10	20.9%
23	29.0%

Apart of the tree of order of 2 (a binary tree), the performance is consistently ~20% worse for insertion of the shuffled sequence (I am aware that “my” 20% drop being close to 25% performance drop mentioned in the article is a happy conincidence, but the drop is there definitely). The order of B-tree is the number of child nodes per internal node. Postgres docs do not say what is the order of its B-trees, and even if it’s constant.

Cache friendliness

Looking at node access times should tell how cache friendly is the insert sequence. The less time between accesses of the nodes, the more is the chance that the node still sits in the cache.

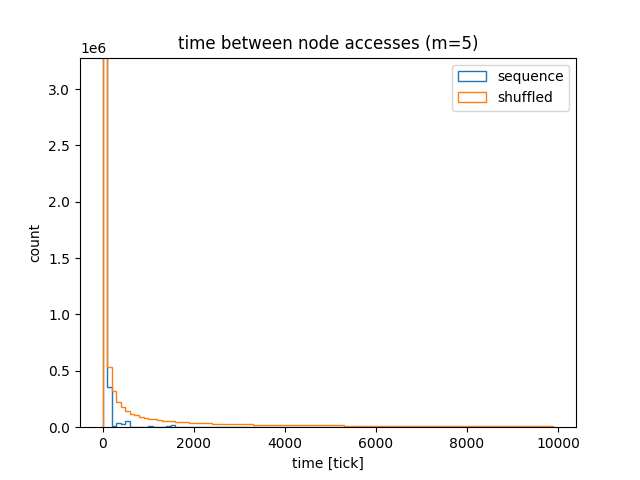
Here are the histograms comparing node access times for a straight sequence and a shuffled sequence. What’s apparent is that for the shuffled sequence, there is a long tail of accesses with large access times.

Zoomed:

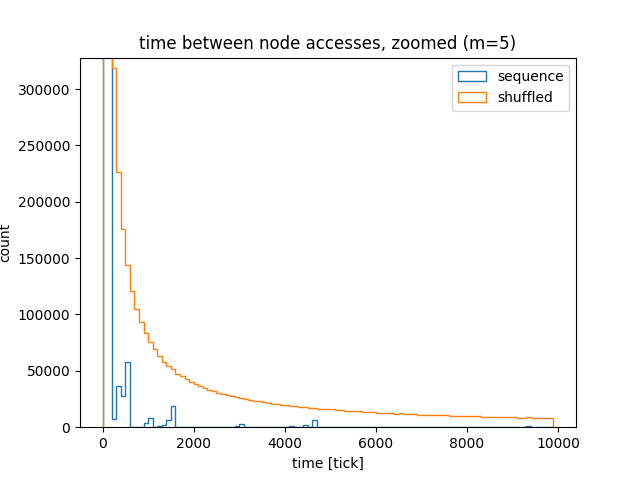
The blue bars on the very left show that most of the nodes were accessed with 2000 “ticks”. This means that if only the cache can hold 2000 nodes, the nodes won’t be evicted from the cache. On the other hand, the orange line shows that there are many nodes that are accessed infrequently, so, intuitively, the chance of cache eviction is higher.

How many?

For the straight sequence, 96% of the accesses happen within 100 ticks, and 99.9% accesses happen within 2,000 ticks. On the other hand, for the shuffled sequence, 47% accesses happen within 100 ticks, 63% within 2,000 and 83% within 100,000 ticks.

Number of rebalances

This article mentions that inserts of UUIDs to MySQL impacts performance because of rebalancing:

With sequential values, this process is relatively straightforward; however, when randomness is introduced into the algorithm, it can take significantly longer for MySQL to rebalance the tree. On a high-volume database, this can hurt user experience as MySQL tries to keep the tree in balance.

I checked that with my simple model. It turns out (at least for the model, I don’t know about MySQL), that for the shuffled sequence, there are less rebalances than for the straight sequence, so keeping the tree in balance does not seem to be an issue. Intuitively, more rebalances for a straight sequence happen because a straight sequence tries to always add a node to the very-right leaf the tree, so the tree is more unbalanced with each insert. In fact, it seems that the straight sequence is the worst case sequence in terms of rebalancing. On the other hand, with the shuffled sequence, the incoming values are “spread” through the leaf nodes, and have a higher chance to land on a node that does not need rebalancing.

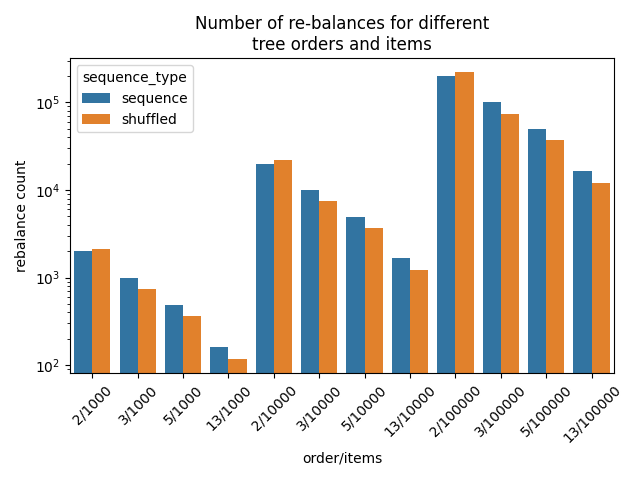
(For a B-tree of order 2 the above does not hold, but I didn’t explore why exactly. I doubt that MySQL used such a low order B-tree though.)

Twist

I wanted to confirm how the cache is affected using Instruments tool, which can track various CPU counters for L1 and L2 cache. I run the benchmarks… and the counters didn’t behave as I expected. I don’t yet know if I misinterpret the CPU counters, or my intuition about the cache is totally wrong. This deserves a separate post.

Takeaways

Using a primary key that results in random accesses to B-tree degrades performance, comparing to serial primary key.